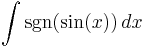Triangle wave

A triangle wave is a non-sinusoidal waveform named for its triangular shape.

Like a square wave, the triangle wave contains only odd harmonics. However, the higher harmonics roll off much faster than in a square wave (proportional to the inverse square of the harmonic number as opposed to just the inverse).

It is possible to approximate a triangle wave with additive synthesis by adding odd harmonics of the fundamental, multiplying every (4n−1)th harmonic by −1 (or changing its phase by π), and rolling off the harmonics by the inverse square of their relative frequency to the fundamental.

This infinite Fourier series converges to the triangle wave:

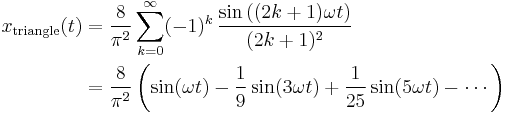
$\begin{align} x_\mathrm{triangle}(t) & {} = \frac {8}{\pi^2} \sum_{k=0}^\infty (-1)^k \, \frac{ \sin \left( (2k%2B1)\omega t \right)}{(2k%2B1)^2} \\ & {} = \frac{8}{\pi^2} \left( \sin (\omega t)-{1 \over 9} \sin (3\omega t)%2B{1 \over 25} \sin (5\omega t) - \cdots \right) \end{align}$

where 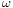$\scriptstyle \omega$ is the angular frequency.

Another definition of the triangle wave, with range from -1 to 1 and period 2a is:

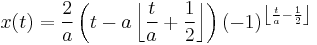
$x(t)=\frac{2}{a} \left (t-a \left \lfloor\frac{t}{a}%2B\frac{1}{2} \right \rfloor \right )(-1)^\left \lfloor\frac{t}{a}-\frac{1}{2} \right \rfloor$

where the symbol 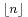$\scriptstyle \lfloor n \rfloor$ represent the floor function of n.

Also, the triangle wave can be the absolute value of the sawtooth wave:

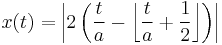
$x(t)= \left | 2 \left ( {t \over a} - \left \lfloor {t \over a} %2B {1 \over 2} \right \rfloor \right) \right |$

The triangle wave can also be expressed as the integral of the square wave:
$\int\sgn(\sin(x))\,dx\,$

References

Weisstein, Eric W., "Fourier Series - Triangle Wave" from MathWorld.

Triangle wave

See also

References